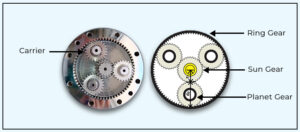
The planetary gear set mostly consists of Four main parts as shown in Figure Below.
- Sun gear
- Planet gear
- Ring gear
- Carrier
Each of these components can be the input, the output, or can be held stationary. Depending upon input, output, and stationery element the following gear ratios can be calculated.
| S.No. | Input | Output | Stationary |
Ratio |
| A | Sun (S) | Planet Carrier (C) | Ring (R) | 1 + R/S |
| B | Planet Carrier (C) | Ring (R) | Sun (S) | 1 / (1 + S/R) |
| C | Sun (S) | Ring (R) | Planet Carrier (C) | -R/S |
Holding any two components together will deliver 1:1 gear reduction. The first gear ratio listed above is a reduction where the output speed is slower than the input speed. The second is an overdrive, where the output speed is faster than the input speed. The last is also reduction but with opposite output direction (hence represented by negative sign).
As most of the industrial applications demand speed reduction, our concern is with only the first type of reduction where the ring gear is held stationary. Input is given through the sun gear and output is the planet carrier.
Let’s look in detail how the Gear ratio is derived for this kind of reduction
- From the basic law of planetary gear set we have,
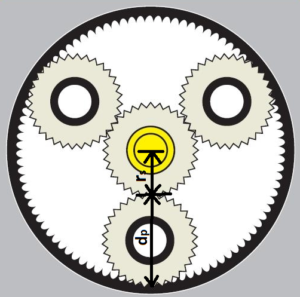
Basic Law of Planetary Gear Set
rr= rs + dp,
rr=rs+ 2rp
2rp= rr-rs – (Eqn. 1)
Where, rr= Radius of Ring Gear,
rs = Radius of Sun Gear,
dp = Diameter of Pinion Gear
rp = Radius of Planetary Gear
Now, we know Linear velocity ‘V’= Angular velocity x Radius = N x r (as ω = 2πN)
Therefore, For an object moving in circle its Linear velocity is V= N x r
- In planetary gear set, as the input is connected to sun gear and output is given to carrier
Gear ratio ‘i’= Ns/Nc
Where, Ns= Speed of Sun Gear, Nc= Speed of Carrier
- Linear Velocity of the carrier is angular velocity x distance from the centre
Vc= Nc x (rs + rp) – (Eqn. 2)
- The instantaneous linear velocity of the point of contact between sun and planet is
Vs= Ns x rs – (Eqn. 3)
Also, instantaneous velocity equals to twice the velocity of carrier
Vs= 2Vc= 2Nc x (rs + rp) – (Eqn. 4)
Equating Eqn. 3 and Eqn.4 we get,
Ns x rs = 2 x Nc x (rs + rp)
i = Ns/Nc = 2 x (rs + rp) / rs
= 2rs + 2rp / rs
From Equation 1 we have,
2rp= rr – rs,
=(2 rs + rr – rs)/ rs
= (rs + rr) / rs
=1 + rr / rs
= 1 + Zr/Zs
Here, Zr is No. Of teeth on Ring Gear, Zs is No. Of teeth on sun gear. Hence Gear ratio for planetary gear set is, Ratio of Number of teeth of ring gear to number of teeth of Sun gear plus One. In this way the gear ratio for planetary gear set is derived…!!